Vibrations
Table of contents
Introduction
In progress
One degree of freedom (1-DOF)
free vibration
damped vibration
forced vibration
Resonanse
Multi-body (n-DOF)
natural frequencies
Every system has as many natural frequencies as there are degrees of freedom. We usually order them by increasing frequency because only first few (lowest frequencies) are important to us. The lowest frequencies have higher amplitude and carry higher energy, while the higher ones are quickly damped to zero.
For real object (not a theoretical model with finite number of elements) there are infinite number of natural frequencies, but as before we care only about first few.
Harmonics
Maybe you heard about harmonic and fundamental frequencies in terms of music, especially guitar strings, and have general knowledge that harmonics are the integer multiplication of fundamental frequencies. But how they are produced? How higher frequencies are introduced to our system?
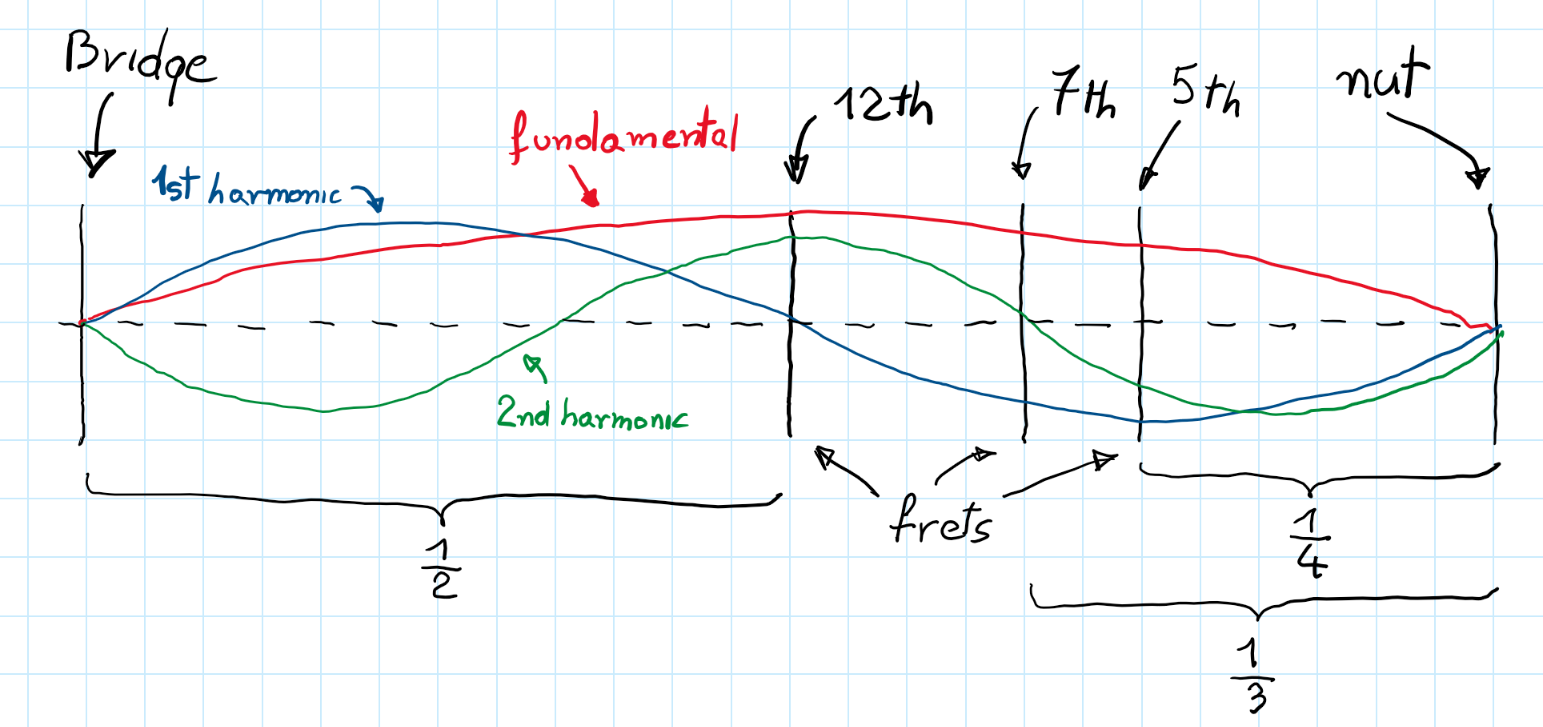
At the beginning let’s focus on guitar string. We know that each string has its fundamental frequency (e.g. note A is $110\ [Hz]$) and it has only one antinode and two nodes (at the bridge and the nut). Those 2 nodes are common for all possible movements of the string so the second possible frequency is $220\ [Hz]$ (1st harmonic) and the next is $330\ [Hz]$ (2nd harmonic). When we strike a string we make it vibrate with many frequencies at once (they are combined into one complex movement). We have to realize that this fundamental frequency(and harmonics) are achieved not because of the frequecy of the input (good luck with sriking the string with $110\ [Hz]$) but from the characteristics of the string (stifness, tension material and so on). With a strike of the string we intorduce some energy into system and this energy is stored as vibrations of the string (and then disipared as a heat). If you want to reduce possible movements you can touch a string at 12th fret (only touching string not fully pressing to the fret). In this way fundamental frequency can not be achieved (also 2nd harmonic or 4th …) and 1st harmonic is the most noticeable. Similarly you can play 2nd harmonic with 7th fret or 3rd with 5th fret.
This case is the exmaple of free vibrations (string is stroke and no additional force are introduced) with dampening (after some time string will stop vibrate).
Drone case
Let us now turn to the mechanical system. Suppose there is a source of the disturbance at $100\ [Hz]$ (e.g. motor on FPV drone). When this vibrations is introduced into the structure it starts to vibrate but like a string not only at one frequency but also at $300 [Hz]$ (although $100\ [Hz]$ is the most pronounced) - why?. So, in ideal scenario if the motor would only interact with a whole system at one point with $100\ [Hz]$ you should get only a $100\ [Hz]$ vibrations in noise measurements. However in reality motor interact with the system more often e.g. it is connected to 3 blade propeller (each time a blade cross over the frame it will add some noise - that’s the source of the $300\ [Hz]$) or a car tire has a really rough tread (It would cause much higher frequency of the noise than frequency of the tire rotation). In summary, all of these additional interaction cause higher frequencies of the noise than we would suspect at the first glance.
The important thing to remember is that although they are present amplitudes of the higher frequencies are usually close to zero and we don’t have to care about them. So filtering only first and second is usually sufficient enought (check RPM filter implementation for a real life example).